摘要:
本论文主要利用单晶金刚石刀具对Cu-Ni合金进行微加工并预测切削刃温度,以此来评估温度是如何影响刀具磨损。通过建立热传导模型、数字温度计算模型和有限元素切屑形成模型,以无量纲的形式来推测温度和切削加工之间的关系。实验还做了蒙乃尔400合金车削加工中刀具磨损的报告,结果显示活化能为53±6KJ/mol。
关键词:金刚石刀具,温度建模,化学磨损
1.引言
采用镜面抛光制造技术并利用金刚石刀具进行微加工工艺已经日臻完善;在对铁和镍进行加工时,由于热活化化学磨损导致的工具寿命降低问题就特别突出,并见诸于一些研究中。
Cu-Ni合金由于其单相的特性,其机械加工性能值得研究,特别是在光学模具工具的应用中。其中有两个问题值得注意:在模压成型制造中是否有一种耐磨的材料组份能较少的引起刀具磨损;随着镍成分的改变,有多少化学工具磨损会发生。
本论文则解决了上述问题,在佩克莱特数小于1时建立工具切屑刃温度预测模型和模拟。工具温度的测量较为困难,但它的量级对热活化磨损较为重要。此外,本研究还利用圆头单晶金刚石刀具对蒙乃尔400进行端面加工并研究其工具磨损等情况,并求得磨损的一个活化能。
2.建模、模拟和确认验证
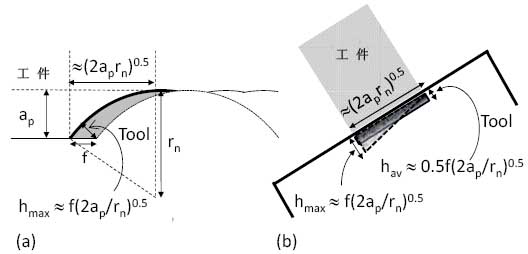
本论文建模和模拟的目的是为了预测与工件发生接触的切削刃周围的温度。图一a为刀头车削加工中未切削的月牙形切屑槽;rn为刀头半径,f为进给,ap为切割深度;未切削切屑厚度h的变化为0~hmax≈f(2ap/rn)0.5;切削刃长度≈(2ap/rn)0.5。图一b为一a的等效图,未切削的切屑槽面积和宽高比与图一a相同,形状为长方形和三角形。
图一:(a)刀头车削平面图;(b)等效图
温度计算的由2D计算和模拟到图一b中的3D切屑形成模拟。图二为一个样例模拟,辅助描述2.1部分的建模。
图二:(a)2D切屑形成模拟;(b)详图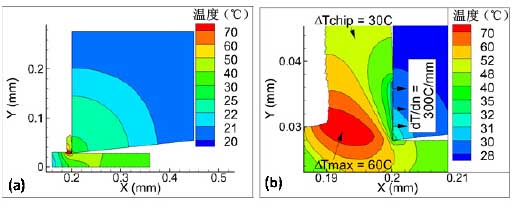
2.1 2D模型和预测
在图二的2D模拟中,h=2μm,切削速度Vc=40m/min,工具导热系数Ktool=1000W/mK,工件导热系数Kwork=22W/mK,蒙乃尔400的热容量ρC=3.8MJ/m3。
图三:(a)概览图;(b)温度计算的分解图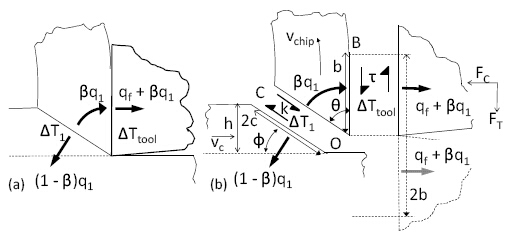
图三为概览图。基础剪切面上的热流q1;一小部分(1-β)流向工件,一部分β流向切屑。所有βq1和摩擦热流qf都流向了工具。图三b为分解图:长度2c的剪切平面OC在ø处沿切削方向倾斜;作用在OC上的剪切应力K;切削速度Vc和切屑速度Vchip;切屑/工具摩擦应力ζ;切削力Fc和轴向力Ft。在本研究中,刀具前角γ=0°。剪切面和前刀面的角度θ=(π/2-ø)。力矩平衡将b和2c关联起来。
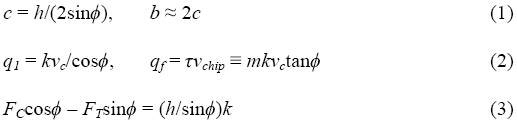
公式4-6分别为ΔTtool、ΔT1和(ΔT1-ΔTtool)。ΔTtool和ΔT1计算方法相同。公式4中比例ft的常量取决于切屑/刀具接触面的宽高比a/b。公式5中fw取决于佩克莱特数B=(hvc)/(4kworktanø).公式6推测计算了从OC到OB的热循环流转。

将公式4、5、6中的ΔTtool和ΔT1置换掉,将公式4中的β回代,得到公式7。左侧是工具温度上升的一种无量纲测量;右侧是系数ft、fw和m、ø、Kwork/Ktool以及FT*/Fc*的函数。
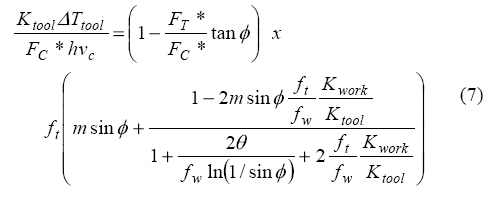
图四描绘了公式7的期望值,首项等于0.85,ft等于3.5,m=0和1,Kwork/Ktool=0.05,ø=10°、20°和30°。横坐标选择取决于fw对B0.5的依赖性。当B<0.2时,在[(hvc)/(4kwork)]0.5的低值处出现的斜面突然变化可以看作fw→ft的近似值。
图四:无量纲工具温度上升对[(hvc)/(4kwork)]0.5的依赖性
2.2 2D温度计算模型和实验结果
本实验建立了一个数字温度计算模型,先假设一个切屑形成的剪切平面模型,如图三所示。输入参数为h, vc, ø,γ, Fc, FT (或者 Fc*, FT*)以此来定义几何形状并计算剪切力和切屑/工具摩擦工作速率以及材料的热物理数据。转化为热量的TQ部分是变化的。图五是根据h,ø,γ自动创建的有限单元网格;工具的直线长度tt和ts以及柄是额外的变量;柄部热边界条件为T=T0。
图五:有限元素温度计算网格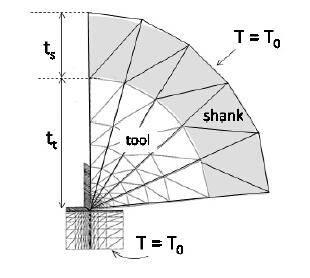
图六:无量纲工具温度上升对[(hvc)/(4kwork)]0.5的依赖性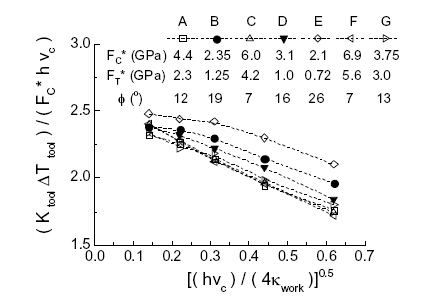
图六为预测切削刃温度,h=2μm、γ=0°、Vc为15-280m/min。工具尺寸tt=100h,TQ=0.9。Fc*和FT*的七个设置A到G以及 ø是输入参量,都产生剪切应力k。但是,工具和柄部尺寸对实验结果都有很大影响。图七为无量纲温度,tt=2mm、ts=25mm。
图七:工具和柄部尺寸对温度的影响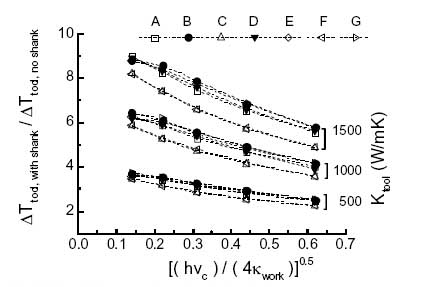
2.3 2D和3D切屑形成模拟
实验利用AdvantEdge软件进行切屑形成模拟。公式8为蒙乃尔400的流动应力,伴随施加的预应力产生的变量。摩擦系数μ在0.25~1.0之间。自小网格大小为0.1h,切割距离和工具尺寸为50-100h。
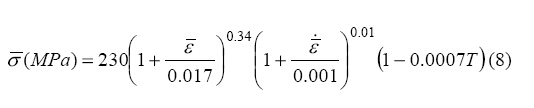
2.3.1 2D模拟
图八为无量纲温度对[(hvc)/(4kwork)]0.5的依赖性,方法及条件和图六相同;结果不完全相同。
图八:利用SCD工具对蒙乃尔400进行切割时无量纲工具温度上升对[(hvc)/(4kwork)]0.5的依赖性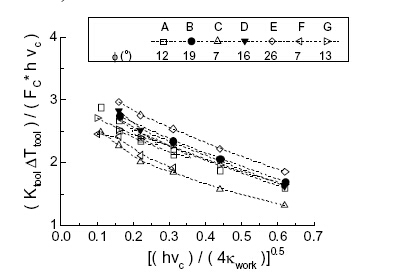
图六中的Fc*、FT*和ø值就来自这些模拟。图九对比了(λ,ø)配对和利用SCD工具进行铜的微加工中的配对。实线为Lee和Schaffer的关系。
图九:λ和ø的关系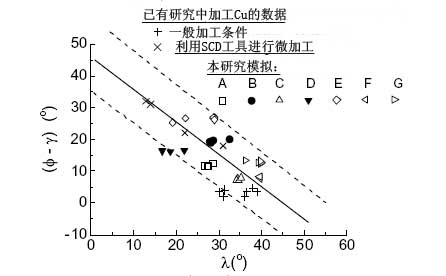
2.3.2 沿切削刃的3D模拟、h常量
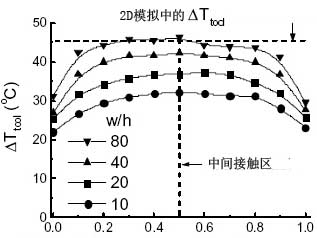
考虑到网格因素,3D模拟中h设置的较高,Vc则较低;hvc保持不变。图10a为h=0.1mm,Vc=2.8m/min,[(hvc)/(4kwork)]0.5=0.44时的概览图;工件宽为1mm。图10b为工具表面温度。图11中,沿切削刃的温度取决于宽高比w/h;温度随w/h的增高而增高,直至w/h=80。
图10:沿切削刃的切屑形成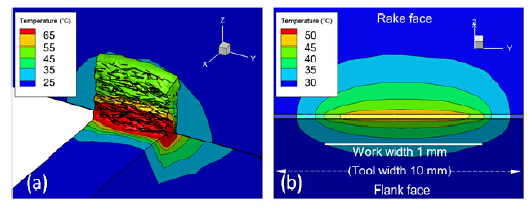
图11
2.3.3 沿切削刃变化的3D模拟和h
除了沿着X轴旋转工具以产生一个三角形未切割切屑横截面外,3D模拟的建立和图10、11相同。h变化由hmin=0到hmax=0.2mm。图12为实验结果。温度沿切削刃变化更加明显并达到最大值。对比图11和12可以看出在中间接触区温度相匹配。
图12:沿切削刃的温度变量对w/hav的依赖性。中间接触区的温度接近hav值(Ktool=500W/mK)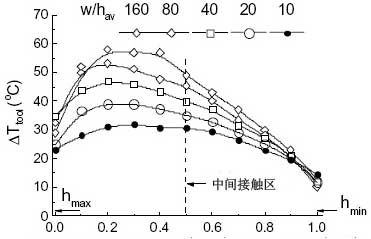
3. 实验和方法
在进给速率为5、15μm/rev条件下对蒙乃尔400圆盘进行端面加工,半径为10-20mm;ap=5μm;工具为半径rn=0.5mm,γ=0°的SCD刀具。在20℃,Ktool=1500±100W/mK条件下对蒙乃尔进行退火。
进给速率hav=0.35/0.1μm,宽高比w/hav=200/67;Vc在125-63m/min之间变化。
切割距离(和时间)随进给速率增大而降低,从f=5μm/rev时的710m降低到f=15μm/rev时的三分之一距离;如图14a所示。
图14:(a)实验几何形状示意图;(b)工具磨损测量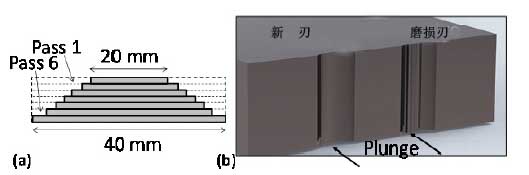
Fc*、Ft*和ø由正交切削实验求得。利用rn=5mm,轴向进给为2μm/rev,速度为67、125m/min的工具对厚度为200μm的蒙乃尔管道进行加工。在室温下进行平面应变压缩实验以求得蒙乃尔400的机械硬化。
4.实验结果
图15为f=5he 15μm/rev条件下切削刃的磨损进程。磨损随进给而增加。
图15:切削刃的磨损进程;f=(a)5,(b)15μm/rev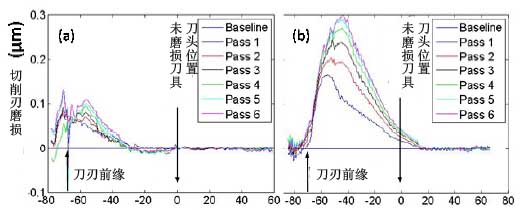
图16为切削刃的磨损随切割时间的变化。选择切削刃的三个不同位置进行观察;磨损随时间呈直线上升。
图16:随时间变化的磨损进程f=15μm/rev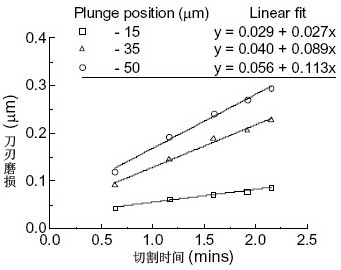
5.结论
SCD工具进行正交微加工工艺中的切削刃初始温度取决于无量纲测量(KtoolΔTtool)/(Fc*hvc)和佩克莱特数[(hvc)/(4Kwork)]0.5。随着工具和柄部的进一步加热,温度上升到了现在温度的8倍。(编译:中国超硬材料网)